
|

|

|

|
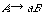
または
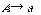
をもつ。ここで大文字の A, B は非終端記号、小文字の a は終端記号である。UNIX で使われる正規表現(regular expression)はこの正規文法をもっており、数学的には記号列をつなぐ連接(concatenation)、記号列のいずれかを選ぶ論理和(disjunction)、0 または任意の回数の連接であるクリーネ閉包(Kleene closure)の3つの演算で定義できる。正規文法はチョムスキー階層で最下層にある。その上の文脈自由文法(context-free grammar)の書換え規則は
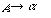
で、左辺は1つの非終端記号でなければならないが、右辺に制約はない。次のレベルが文脈依存文法(context-sensitive grammar)で、その書換え規則は
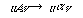
の形をしている。最も一般的な文法は、全く制約のない書換え規則
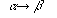
をもつ無制約文法(unrestricted grammar)である。
よく知られているように、形式文法で生成される言語はオートマトンと密接な関連がある。正規言語は有限オートマトンと、文脈自由言語はプッシュダウンオートマトン(pushdown automaton)と、文脈依存言語は線形有界オートマトン(linear bounded automaton)と等価である。無制約文法による言語は帰納的可算(recursively enumerable)で、チューリングマシン(Turing machine)に一致する。
さて、形式文法の考え方はDNA、RNA、タンパク質の解析に実際どの程度有効であろうか。コンセンサス配列の表現あるいはコンセンサス配列による検索は正規文法、すなわち有限オートマトンや正規表現が有効であった。一方、パリンドロームやRNAのループ構造は正規文法では表現できず、文脈自由文法になる。そこで、文脈自由文法の書換え規則に確率を付与した統計的文法を用いると、隠れマルコフモデル(確率オートマトン)では記述できないRNA二次構造予測の問題を扱うことができる。なお、RNAのシュードノットを表現するには文脈依存文法が必要である。データ(例文)から学習によって文法を獲得する方法は知られており、これまでに述べてきた様々な方法と同様に、配列の特徴を学習して構造・機能予測に適用することが可能である。タンパク質立体構造形成の階層性や遺伝子発現の階層性を始め、配列より高次の生物学の問題が、文法あるいはそれと等価な方法で記述できるかは興味深い問題であるが、現状ではまだ未知数である。