
|

|

|

|
タンパク質の立体構造解析のために、X線結晶解析やNMRによる立体構造データを出発点とし、古典力学的な取り扱いによる分子全体の静的構造および動的構造の計算、量子論的な取り扱いによる機能部位などの局所構造および相互作用の計算が、従来から盛んに行われている。これら物理・化学の原理に基づく計算に対し、立体構造データベースの増大とともに、本書で述べてきたような計算機科学的な方法を適用し、経験的な法則を発見しようとするアプローチが盛んになってきた。その1つは立体構造パターン認識の問題である。配列アライメントの方法が配列の類似性を調べたり、グループ内で共通の配列パターン(配列モチーフ)を探すために用いられるのと同様に、立体構造アライメントの方法は立体構造の類似性を調べたり、共通のフォールドパターン(構造モチーフ)を探すのに用いられる。具体的に立体構造アライメントをどのように行うかについては実に多様な方法が提案されているが、ここでは巻末に参考文献を列挙するにとどめる。
もう1つ、ゲノム情報との関連から重要な問題は、一次構造から立体構造を予測することである。ここでも以前の物理化学的な方法に対し、実際のデータに基づく経験的な方法が主流となった。これは分子進化の経験的知識として、「配列が似ていれば立体構造も似ている」ことを前提として解析を行う。実際、2つのタンパク質が同じファミリーやスーパーファミリーに属す場合、すなわち2つのアミノ酸配列の間に有意なホモロジーがある場合は、両者の立体構造もよく似ている。従って、構造予測を行うタンパク質のアミノ酸配列を、立体構造データベースのアミノ酸配列に対してホモロジー検索を行い、もし立体構造既知のタンパク質と有意な配列ホモロジーが見つかれば、それをもとに立体構造のモデルを作ることができる。これをホモロジーモデリング(homology modeling)という。 ホモロジーモデリングは分子進化的な意味も明らかであり、立体構造予測の最も確実な方法であるが、現実にはホモロジーが見つからず予測できない場合が多い。そこでホモロジーの意味をもっと弱い類似性にまで拡張し、予測できる場合を多くしようとするのが3D−1D法である。その根拠は立体構造データの増加とともに、配列のホモロジーがないにもかかわらず立体構造が類似のタンパク質が見つかるようになってきたことである。これには2つの側面があり、1つは本来進化的に関連のあるタンパク質が遠く離れすぎてしまったためホモロジーが見えなくなっている可能性、もう1つはポリペプチド鎖の物理化学的な性質から異なるアミノ酸配列が類似のフォールドをとっている可能性である。
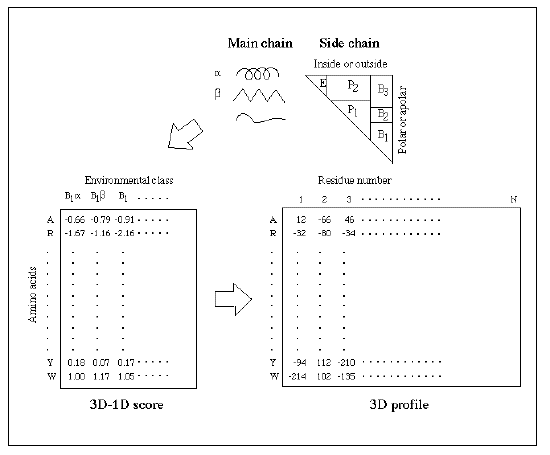
3D−1D法では、既知の立体構造のライブラリーの中でどの構造が与えられたアミノ酸配列に適合するか、立体構造と一次構造の適合性を評価して調べる。従って、立体構造のライブラリーを作ることと、配列−構造適合性評価関数を作ることが基本である。ここでは Eisenberg らの方法に基づいて簡単に概念を説明する(図参照)。まず、立体構造中でアミノ酸が置かれている環境を、3つの二次構造状態と6つの側鎖の状態から合計18のクラスに分類する。これにより1つの立体構造は18の記号からなる1つの記号列に変換することができる。次に立体構造既知のタンパク質(およびホモロジーのあるタンパク質)で各アミノ酸が各クラスに存在する頻度を調べ、3D−1Dスコアのマトリックスを定義する。環境クラスの記号をこのマトリックスの対応するカラムに変換し、記号列で表現された1つの立体構造は1つの数値カラム列、すなわち3Dプロファイルとして表現される(図参照)。与えられたアミノ酸配列がどの立体構造と最も適合するかは、3Dプロファイルライブラリー中で、3D−1Dアライメントの評価値が最も高いものを探すことで分かる。ここで一般には、アミノ酸の欠失・挿入があり得るので、この手続きはダイナミックプログラミング法を用い、ギャップペナルティも定義しておかなければならない。このように3D−1D法は、機能部位のプロファイルを作ってモチーフ検索を行う手続きと非常に類似していることが分かるだろう。プロファイルを確率とする見方では、アミノ酸がどの立体構造の環境のもとにあるかを事前に知っているので、これを事前確率として導入しベイズの法則により事後確率を高めたことに相当する。
タンパク質をファミリー、スーパーファミリー、フォールドと分類すると、1D−1Dアライメント(ホモロジー)はスーパーファミリーまで、3D−1Dアライメントはフォールドまでの類似性を検出できる。自然界にフォールドが何個あるかはもちろんまだ分からないが、乱暴な議論によれば数千のオーダーしかなく、これを全部X線結晶解析やNMRで決めてしまえば、タンパク質立体構造予測の問題は解決したことになるという。フォールドがこれまでにいくつ解明され、毎年いくつずつ増加し、最終的にいくつになるかが分かれば、何年後に構造予測の問題が解決するか予測できるわけだ。もっとも、フォールドが全部決まる頃には、すべてのスーパーファミリーの立体構造も解明されており、3D−1D法よりも正確なホモロジーモデリングで立体構造予測が解決することになるのかもしれない。