
|

|

|

|
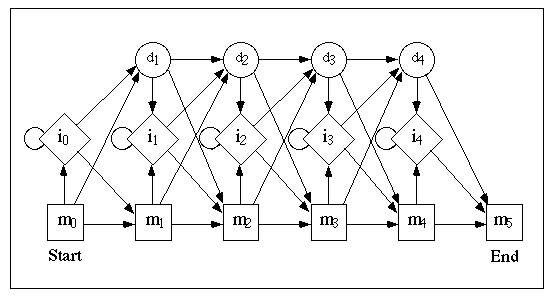
BLASTアルゴリズムの所で述べた有限オートマトンを拡張し、状態遷移が確率的に起こるとしたオートマトンを確率オートマトン(probabilistic automaton)という。その一種として、音声認識で使われてきた隠れマルコフモデル(HMM: hidden Markov model)は、マルコフ連鎖(Markov chain)の各状態に記号の出力確率を与えたもので、配列のパターン認識にも非常に有効である。上図に1つのモデルが書かれている。ここで、m0 は初期状態、m5 は最終状態で、m1 から m5 まで四角で示した状態は配列中または配列アライメント中の位置を示し、それぞれに塩基配列であれば4種の、アミノ酸配列であれば20種の記号の出力確率が存在する。配列には欠失・挿入が起こることを考慮し、図では主状態である mk 以外に、記号の欠失状態 dk と挿入状態 ik が書かれている。挿入状態にはやはり記号の出力確率が存在するが、欠失状態は記号が出力されないダミー状態である。このように、塩基配列やアミノ酸配列はマルコフ連鎖によって記号列が生成されていると仮定するが、マルコフ連鎖の状態遷移の様子は直接には見えない(モデルの状態遷移図には記号の出力が書かれていない)ので、「隠れ」マルコフモデルというのである。
図のような特定のモデルは多数の配列パターンを生成する。生成された個々の配列パターンには状態遷移確率と記号出力確率から計算される確率が付随している。一般に同じ配列が複数の経路から生成され得るので、それらを足し合わせたものが1つの配列に対する確率である。いま、隠れマルコフモデルを機能部位予測に適用することを考えると、機能部位の配列グループに対してだけ高い確率を与えるようなモデルを見つけることが問題となる。これはトレーニングデータセットに学習アルゴリズムを適用し、隠れマルコフモデルのパラメタである状態遷移確率と記号出力確率を最適化することにより、また場合によってはモデルの長さも最適化することにより解くことができる。
いま、トレーニングの配列データ s(1), s(2), ..., s(n) が与えられたときに、これが モデルにどの程度適合するかは、それぞれの配列が同時に起こる確率であるので
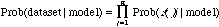
で評価する。これは、最尤(ML: maximum likelihood)法の考え方である。もう1つの考え方では、ベイズの法則により最大事後確率(MAP: maximum a posteriori)

を用いて評価する。ここで、Prob(model) は事前確率、Prob(dataset) は規格化のための定数である。MAP は最小記述長(MDL: minimum description length)にも通じる考え方で、モデルの複雑さ(確率として表現されている)を加味してトレーニングデータへの適合性を決める。つまり、あまりにも複雑なモデルでトレーニングデータにぴったり合わせるよりも、単純なモデルでトレーニングデータがそこそこ合えばよいという考えである。
隠れマルコフモデルの学習アルゴリズムは次のような逐次的方法である。まず、適当な初期モデルを選ぶ。トレーニングデータセットの各配列について可能な経路をすべて調べ、実際に起こる状態遷移の頻度と記号出力の頻度をもとに、ML または MAP の意味で遷移確率と出力確率を更新して次のモデルとする。この手続きを更新がごくわずかになるまで繰り返す。ところで、隠れマルコフモデルは確率的な意味で作られたプロファイルと非常に近い関係にある。隠れマルコフモデルの方が欠失と挿入を明確に定義しているため多少一般的であるが、その記号出力確率はまさにプロファイルである。隠れマルコフモデルの学習アルゴリズムは、期待最大化(EM: expectation maximization)と呼ばれる方法の一種であり、実際この考え方でプロファイルを逐次的に更新していく方法が提案されている。とくに、ギッブスサンプリング(Gibbs sampling)と呼ばれる方法では、メトロポリスモンテカルロやシミュレーテッドアニーリングにも通じる熱平衡分布への緩和の考え方を取り入れた扱いがされている。