
|

|

|

|
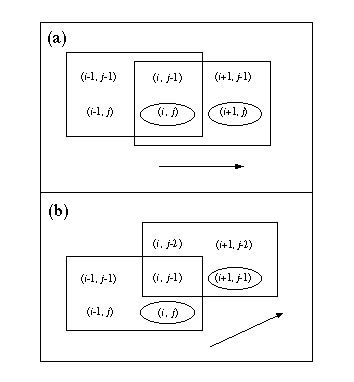
ホモロジー検索は問合せ配列(query sequence)と類似な配列がないかデータベースを調べることである。ここで類似な配列とは局所的に類似な部分をもった配列で、データベース中の配列を1つずつ取り出し、問合せ配列とペアワイズにローカルアライメントを行って調べる。ダイナミックプログラミング法によるペアワイズアライメントは O(n2) のアルゴリズムであるので、例えば 103 ベースのDNA塩基配列を 109 ベースある GenBank データベースに対してホモロジー検索すると、1012 の演算が必要になる。ダイナミックプログラミング法はこのように長時間の計算を要するが、厳密に最適な解を与えるので最も精度の高い方法でもある。塩基の一致・不一致のみで評価関数が作られるDNAのホモロジー検索は次に述べる高速検索法で十分であるため、ダイナミックプログラミング法はほとんど使われない。しかし、アミノ酸置換行列で評価するタンパク質の場合はデータベースがDNAほど大きくなく、また精度が重要であることが多いため、ダイナミックプログラミング法をうまく高速化してホモロジー検索が行われる。 高速化の鍵は並列処理である。マトリックス要素 Di,jを計算する際、普通は図(a)に示したように各行左から順番に計算していくだろう。すると Di+1,j の計算には Di,j の値が必要なため、Di,j の計算が終わってからでないと Di+1,j の計算ができない。つまり、この場合は逐次処理しかできない。一方、図(b)では Di,j を反対角線方向の順番で計算しており、図から明らかなように Di,j と Di+1,j-1 など1つの反対角線上にある要素はすべて同時に計算できる。つまり並列処理が可能なのである。実際、この並列アルゴリズムはベクトル型スーパーコンピューターに実装して、有効性が確かめられている。ただし、反対角線の長さは変化し平均としてそれほど長くないので、いわゆるベクトル化率は高くない。 ホモロジー検索のもう1つのタイプの並列処理として、アルゴリズムを並列化するのではなくデータベースを分割することが考えられる。これは分散メモリー方式の超並列計算機やワークステーションのクラスターなどで有効な方法である。各プロセッサにデータベースの一部ずつを担当させて検索を行うだけのことであるが、プロセッサの台数効果が直接反映するので、今後データベースがますます大きくなるにつれて必須のアプローチとなるだろう。
ところで、ホモロジー検索の結果は評価関数の値であるホモロジースコアや、アライメントを作ったときの文字の一致の割合などでスクリーニングを行って解釈される。スコアが非常に高い場合は問題なく類似性があると言えるだろうが、トワイライトゾーンと呼ばれる弱いホモロジーの領域では統計的に有意かどうかを調べる必要がある。いま2つの配列のアライメントから得られたホモロジースコアが S であったとする。それぞれの配列で文字の順番をランダムに並べ替えた配列を作ってアライメントを行う手続きを n 回繰り返すと、ランダム配列でのホモロジースコア s1, s2, ..., sn が得られる。その平均値をμ 、標準偏差を σ とすると、
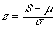
は、実際の配列でのスコアが同じ組成のランダム配列でのスコアと比較してどの程度有意かの指標となる。ランダム配列のスコアが正規分布に従うとすると、z スコアが4または5である確率はそれぞれ 3 x 10-5 または 3 x 10-6 となる。
ランダム配列を何百回、何千回と生成して統計的有意性の評価を行うことは特定のアライメントの解析には有用であるが、計算時間の観点からホモロジー検索の一部に組み込んで行われることはまずない。アミノ酸配列のトワイライトゾーンの目安としては、アライメントの長さが 50 残基以上で、アミノ酸の文字の一致が30%以上あれば、経験的に有意なホモロジーと考えて良さそうである。もちろんアライメントの長さがもっと短かったり、一致度が20〜30%しかなくても有意なことは十分にあり得る。また、統計的に有意であることと生物的に有意であることは必ずしも一致しない。統計解析はあくまでも生物的に意味のあるものを見いだすための一手段として考えるべきであり、類似性が見つかった部分は機能部位と関連があるか、システインのような重要な残基が一致しているかといった生物的な考察が必要である。