
|

|

|

|
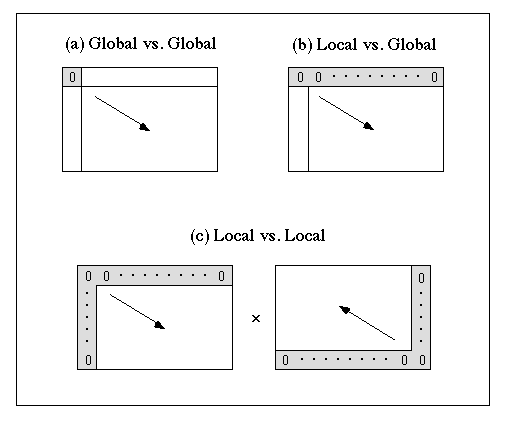
以上のように経路マトリックスの左上端から右下端までに相当するアライメントは配列全体のアライメント、すなわちグローバルアライメントである。では、ローカルアライメントはどのように求めることができるだろうか。図に1つの方法を示した。グローバルアライメントは D0,0 の要素のみ初期値 0 にして計算した。つまり横方向配列と縦方向配列の左端を揃えた状態から比較を開始するのである。一方、図(b)にあるように D0,j = 0 (j = 1〜m) とすると、縦方向の配列に対し横方向の配列をどこから比較し始めてもペナルティがかからないことになる。例えば横方向配列は2つの重複したドメインからできていて、それぞれが縦方向配列に類似している場合でも、両方検出することができる。従ってこの場合、縦方向配列にとってはグローバルアライメントだが横方向配列にとってはローカルアライメントをしていることになる。 この考えを進めていくと、Di,0 = 0 (i = 1〜n), D0,j = 0 (j = 1〜m) としてやれば両配列とも端のずれに対してペナルティがかからず、ローカルアライメントができるのではないだろうか。Sellers は図(c)に示したように、この手続きを順方向と逆方向に2回配列比較を行い、経路マトリックスで両者の論理積をとることを提唱した。しかしながら、この考えだけではローカルアライメントはうまく検出できず、初期値 0 を図のマトリックスの内部にまでうまく取り込むことが必要である。いま置換行列要素 wi, j が類似であるか否かにより正(得点)と負(減点)の値からなり、ギャップコストも負(減点)であるとする。ここで、評価関数は
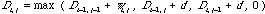
のように、0 を加えて最大値をとる。すなわち、評価関数の値が負になれば強制的に 0 にし、その場合には経路を作らないことにするのである。すると新たに類似領域があった場合、初期値 0 から再出発できるとともに、新たに経路が生成されることになる。Smith-Waterman アルゴリズムではこの考えに基づき、Di,j が最大になった所からトレースバックを行って最適のローカルアライメントを求める。Goad-Kanehisa アルゴリズムではこの考えに Sellers 流の両方向アライメントの論理積を加えて、ある基準以上のローカルアライメントをすべて求めることができる。