
|

|

|

|
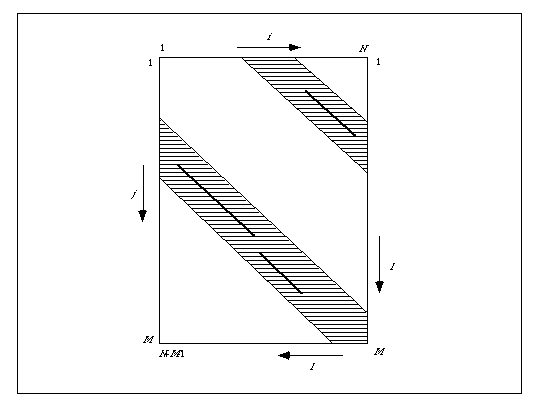
いま比較する2本の配列を、左上を原点として横方向と縦方向に並べたマトリックスを作り、一致する文字ペアの位置に点(ドット)をうつと、局所的に文字が連続して一致している部分は対角線の線分要素として検出することができる。これをドットマトリックス(dot matrix)といい、普通は文字単位ではなくある長さのウインドウをとってノイズを減らす操作を加味して利用されている。ところで上の図に示したように、このようなドットマトリックスの中で、局所アライメントに相当する対角線分が現れる領域は非常に限られており、実は O(n2) のアルゴリズムであるダイナミックプログラミング法でマトリックス全領域を計算することは、結果的にはかなり無駄をしていることになる。 そこで、まず何らかの方法で対角線分が現れる位置を高速に探したとしよう。この位置はダイアゴナルと呼び、図では 1 から N+M-1 までの値をとる l で指定される。欠失・挿入の可能性を考え、見つかったダイアゴナルのまわりに適当な幅をとり、限られた領域(図で斜線をつけた部分)にのみダイナミックプログラミングを適用すると、計算量は面積に比例するので大幅な高速化ができることになる。FASTAアルゴリズムはこのような考えと、最初の高速ダイアゴナル検出にハッシング(hashing)というテクニックを使ったアルゴリズムである。
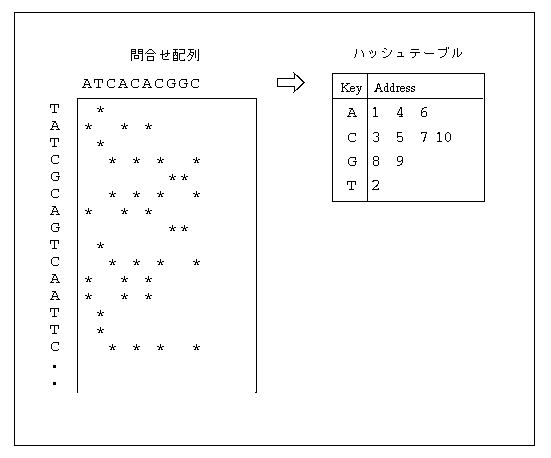
ハッシングは計算機科学の様々な探索問題に適用される一般的なアルゴリズムで、特殊なテーブルを参照することにより高速検索を行うものである。上図にその概念図を示した。ここではホモロジー検索の問合せ配列が横方向に、データベースの配列が縦方向に書いてある。データベース中の配列をすべてつないで考えると縦方向は非常に長い配列を表現していることになる。さて、これからドットマトリックスを作ることを考えると、まず最初の行でTを左から1文字ずつ比較し、次の行でAを同様に左から1文字ずつ比較し、といったことを繰り返すことになる。つまり横方向の配列に対して何度も何度も同じ手続きを繰り返すことになる。そこで、横方向の配列に前処理をほどこし、高速化を考えてみよう。配列が塩基配列だとすると4種類の文字しかないのだから、それぞれの文字(キー)が何番目に現れているか(アドレス)のハッシュテーブルに変換するのである(図)。すると、例えば縦方向の配列の文字がAであれば、テーブルを参照することによりドットをうつべき場所がすぐに分かり、他の文字との無駄な比較をしなくてもすむ。計算時間は各文字に対するテーブルの長さに比例し、塩基組成が均等であるとするとこれは問合せ配列の長さの1/4になるので、4倍のスピードアップが得られることになる。
ハッシュテーブルは1文字単位でなく、2文字以上の単位のキーに対して作ることもでき、さらにスピードアップを図ることができる。FASTAプログラムではこれをパラメタとし、k-タプル(k-tuple)と呼んでいる。例えばタプルサイズが2の場合つまりダブレットを考えると、塩基配列では16種類があるので16倍のスピードアップになる。ただし、当然のことであるがダブレットの2文字とも一致しなければ検出できないので、例えば AC と AG が半分一致しているといったことは分からなくなってしまう。すなわち、タプルサイズを大きくすると検索は高速になるが感度は悪くなるのである。FASTAプログラムでは k-タプルのデフォールト値を、塩基配列の場合6にアミノ酸配列の場合2にとってある。