
|

|

|

|
ダイナミックプログラミングの原理を理解した上で、実際の配列比較を考えてみよう。まず重要なことは類似性の尺度である。塩基配列の比較の際には単に文字の一致・不一致で点数付けを行うことが多い。一方、アミノ酸配列の比較にはアミノ酸の類似度を考慮したアミノ酸置換行列が用いられる。下の表に最も代表的なアミノ酸置換行列である PAM250 マトリックスを示した。これは Dayhoff マトリックスとも呼ばれ、Dayhoff らがチトクロームやグロビンなどのファミリーに属するタンパク質の配列を多数集め、進化上の関連解析から置換の頻度を調べて作ったものである。最適化の評価関数を定義するにはこのような点数表以外に文字の欠失に対する点数、これをギャップペナルティという、が必要である。
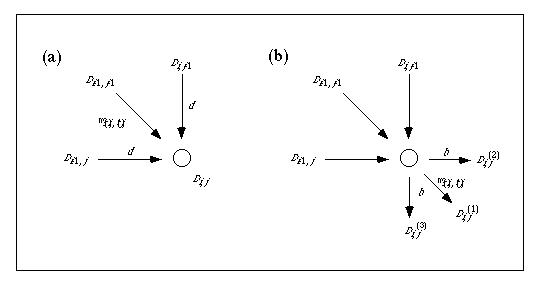
いま置換行列に相当する点数表の値を wi, j で表現し、1つの欠失の点数を d とする。ダイナミックプログラミング法では、各ノードでの評価関数の値 Di,j は斜め方向、横方向、縦方向の3つの経路の中から最適のものを選ぶことによって決定される(図参照)。これを式で書くと
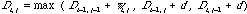
となる。初期値を D0,0 = 0, Di,0 = i d (i = 1〜n), D0,j = j d (j = 1〜m) とし、経路マトリックスの左上端から順番に Di,j を計算していって右下端に到達したときの値が最適の評価関数値である。この計算を各ノードでしながら同時に3つの可能性の中からどの経路(複数のこともあり得る)をたどった場合に最適であったかを覚えておき、今度は右下端から最適経路を逆向きにたどる(トレースバックする)ことにより最適アライメントを作ることができる。全体で n x m の定数倍に相当する計算が必要なことから、これは O(n2) のアルゴリズムである。上記の形とは多少異なるが、このアルゴリズムを最初に提案したのは Needleman-Wunsch である。
ところで塩基配列やアミノ酸配列に欠失・挿入が起こる分子メカニズムを考えると、連続したギャップは長さによらずに1度に起こる可能性が高い。しかしながら上記のギャップペナルティの与え方では、2文字連続のギャップは1文字のギャップの2倍のペナルティが与えられ、欠失・挿入が2度起こったことに相当する扱いがされている。そこで、ギャップについては現実の分子メカニズムを反映したペナルティを定義することが望ましい。もし一般にギャップの長さ k に対してペナルティを dk と定義すると、上の式は
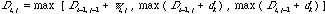
となり、二重の max 操作のため O (n3) のアルゴリズムになってしまう。そこで、普通は a + b k のように長さ k に線形に比例する形で与える。すると、各ノードで斜め方向、横方向、縦方向に対応して3つの値を覚えておけば、
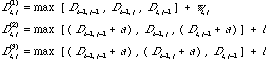
のように、O(n2) のアルゴリズムのままですむ。ここで、斜め方向に進む場合は3つの可能性の中で最適なものに要素 i, j の類似度 wi, j が加えられる。横方向と縦方向は、すでにあるギャップをのばす場合はコスト b が加えられ、新たなギャップが始まる場合は a + b が加えられて、最適なものが選ばれる(上図参照)。
| Ala | 2 | |||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Arg | -2 | 6 | ||||||||||||||||||
| Asn | 0 | 0 | 2 | |||||||||||||||||
| Asp | 0 | -1 | 2 | 4 | ||||||||||||||||
| Cys | -2 | -4 | -4 | -5 | 12 | |||||||||||||||
| Gln | 0 | 1 | 1 | 2 | -5 | 4 | ||||||||||||||
| Glu | 0 | -1 | 1 | 3 | -5 | 2 | 4 | |||||||||||||
| Gly | 1 | -3 | 0 | 1 | -3 | -1 | 0 | 5 | ||||||||||||
| His | -1 | 2 | 2 | 1 | -3 | 3 | 1 | -2 | 6 | |||||||||||
| Ile | -1 | -2 | -2 | -2 | -2 | -2 | -2 | -3 | -2 | 5 | ||||||||||
| Leu | -2 | -3 | -3 | -4 | -6 | -2 | -3 | -4 | -2 | 2 | 6 | |||||||||
| Lys | -1 | 3 | 1 | 0 | -5 | 1 | 0 | -2 | 0 | -2 | -3 | 5 | ||||||||
| Met | -1 | 0 | -2 | -3 | -5 | -1 | -2 | -3 | -2 | 2 | 4 | 0 | 6 | |||||||
| Phe | -4 | -4 | -4 | -6 | -4 | -5 | -5 | -5 | -2 | 1 | 2 | -5 | 0 | 9 | ||||||
| Pro | 1 | 0 | -1 | -1 | -3 | 0 | -1 | -1 | 0 | -2 | -3 | -1 | -2 | -5 | 6 | |||||
| Ser | 1 | 0 | 1 | 0 | 0 | -1 | 0 | 1 | -1 | -1 | -3 | 0 | -2 | -3 | 1 | 2 | ||||
| Thr | 1 | -1 | 0 | 0 | -2 | -1 | 0 | 0 | -1 | 0 | -2 | 0 | -1 | -3 | 0 | 1 | 3 | |||
| Trp | -6 | 2 | -4 | -7 | -8 | -5 | -7 | -7 | -3 | -5 | -2 | -3 | -4 | 0 | -6 | -2 | -5 | 17 | ||
| Tyr | -3 | -4 | -2 | -4 | 0 | -4 | -4 | -5 | 0 | -1 | -1 | -4 | -2 | 7 | -5 | -3 | -3 | 0 | 10 | |
| Val | 0 | -2 | -2 | -2 | -2 | -2 | -2 | -1 | -2 | 4 | 2 | -2 | 2 | -1 | -1 | -1 | 0 | -6 | -2 | 4 |
| Ala | Arg | Asn | Asp | Cys | Gln | Glu | Gly | His | Ile | Leu | Lys | Met | Phe | Pro | Ser | Thr | Trp | Tyr | Val |