
|

|

|

|
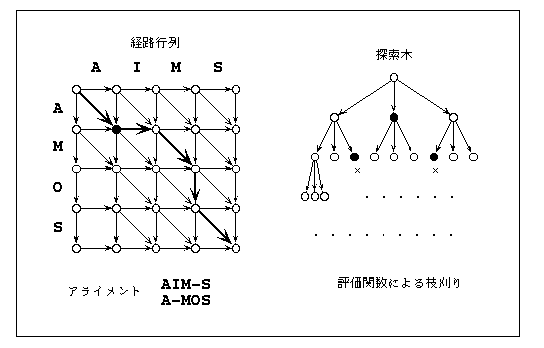
配列解析の出発点は、ダイナミックプログラミング(DP: dynamic programming)法による2つの配列アライメントを理解することである。いま2つの文字列が与えられたときに、適当な場所にギャップを入れてずらすことにより、両者で対応する文字の一致数が最大になるような並べ方を探してみよう。上の図に2つの文字列AIMSとAMOSを例として、ダイナミックプログラミング法の原理が示されている。この場合
AIM−S A−MOSのように−で示した位置にギャップを入れて並べると3つの文字が一致する。これが最大の一致数に対応したアライメント、すなわち最適アライメント(optimal alignment)で、この問題の解となる。アライメントの問題とは結局、ある評価関数(この例では文字の一致数)を最適にする最適化問題に帰着するのである。
ダイナミックプログラミング法による解法は、比較する配列を横方向と縦方向に並べたマトリックスの形で説明される(図の左側)。両者の配列を左から順に並べていく操作には3つの可能性がある。横方向の配列から1文字と縦方向の配列から1文字をもってきて並べる場合、横方向の配列のみから1文字をもってくる(縦方向にギャップを入れる)場合、縦方向の配列のみから1文字をもってくる(横方向にギャップを入れる)場合の3つである。これは図のマトリックスの中で丸印で示したノードから3つの矢印が出ていることに相当する。斜め方向の矢印が両方の配列から文字をもってくる場合、横方向の矢印が横方向の配列のみからもってくる場合、縦方向の矢印が縦方向の配列のみからもってくる場合である。マトリックスの左上端のノードから右下端のノードまで行く1つの経路が1つのアライメントに相当し、最適アライメントを探す問題は最適経路を探す問題と同等になる。図の右側にある探索木は経路がどのように分かれていくかを示したもので、1つのノードから3つずつ分かれていくので、配列が長くなればなるだけ膨大な数の組合せが生まれることになる。配列アライメントの問題は組合せ最適化(combinatorial optimization)問題なのである。
このような探索木の中から解を探す問題は人工知能の分野でしばしば見られ、探索木の深さ優先で探す縦型探索や幅優先で探す横型探索を始め、多くの探索法が知られている。配列アライメントの問題は、パズルのようにたくさんあり得る解の中からどれでもいいから1つを高速に探すのではなく、与えられた評価関数で最適な値をもつものを探す必要があり、ダイナミックプログラミング法はそのための一般的な解法である。ダイナミックプログラミング法の原理は次のように理解することができる。図のマトリックスで、左上端のノードから斜め下の黒丸で示したノードへ行く経路は3通りあり得るが、それぞれには評価関数の値が付随している。いま直接斜めに行く経路の方が右と下あるいは下と右をたどって行く経路より評価関数の値がよかったとすると、探索木で×印をつけた所の下の部分は探索する必要がないことになる。つまり評価関数により探索木の枝刈りをすることができるわけで、これがマトリックスの各ノードで行われるため、組合せの数を大幅に減らすことができる。ダイナミックプログラミング法による2つの配列アライメントの問題では、このように実質的にすべての組合せでの値を勘定して最適なものを探すので、厳密解を得ることができるのである。
2本の配列のアライメントは概念的には簡単にn本の配列のアライメント、すなわちマルチプルアライメントに拡張することができる。それは2次元のマトリックスをn 次元のマトリックスに拡張することで、例えば3本なら図の縦方向と横方向にさらに垂直方向の軸を加えて立体的なマトリックスを作ればよい。3本のダイナミックプログラミングは実用上も充分に可能であるが、配列の本数が増えると急激に組合せの数が爆発し、厳密解を得ることが難しくなる。従って、一般にマルチプルアライメントでは組合せ最適化問題の近似解法を適用する必要がある。