
|

|

|

|
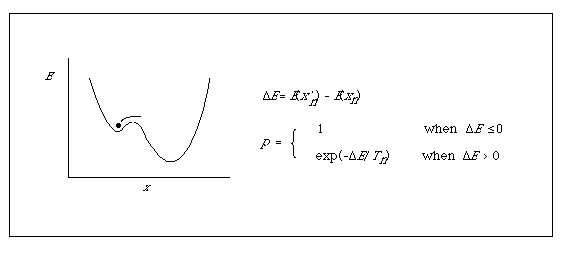
ここで、最適化問題を少し別の観点から考えてみよう。図は最適化の評価関数の形を模式的に示したものである。横軸は配列比較の場合、可能なアライメントの空間を示している。最適化問題とは評価関数の最適値を探す問題である。ここではこれまでの評価関数と符号を逆にしているので、とくにエネルギー関数 E と呼ぶことにすると、エネルギーの最小値を探すことが問題である。この絵のようにエネルギー関数の全体像が分かっていればどこに最小値、すなわちグローバルミニマム(global minimum)があるかは明らかである。しかし、複数配列アライメントのように組合せの数が膨大になると全体像を計算することができないので、現在のアライメントの形が計算できる範囲内で他の形よりエネルギー値がいいからといって、それが全体の最小値なのか、局所的な最小値なのか区別がつかない。大規模な組合せ最適化問題にはこのローカルミニマム(local minimum)の問題が常に困難として伴っている。
ローカルミニマムに捕まらないでグローバルミニマムを探す一般的な方法として、シミュレーテッドアニーリング(SA: simulated annealing)がある。アニーリングとは鉄などの焼きなまし過程のことである。鉄をまず高温に熱した後、徐々に冷却すると強い鉄つまり安定な結晶状態の鉄ができるが、急激に冷却するともろい鉄つまり準安定状態の結晶になってしまう。これは図のグローバルミニマムとローカルミニマムに対応しており、熱運動を利用してローカルミニマムからうまく脱出させ、グローバルミニマムに到達させるのがアニーリングである。
それでは複数配列アライメントの問題にシミュレーテッドアニーリングを適用してみよう。これも人間がアライメントするやり方を思い浮かべると、恐らく適当な場所に適当な変更を加えて全体としてアライメントがよくなったかどうかを判定し、よければ次に進み悪ければやり直すことを繰り返すだろう。同様にシミュレーテッドアニーリングではアライメントの初期状態から出発し、ある配列のある部分を動かすといった微小変形を順次適用していく。微小変形でエネルギー値(評価関数の値)がよくなればもちろん変形は受け入れるが、もし悪くなれば受け入れないとすると、ローカルミニマムから脱出できない。そこで悪くなった場合でも以下の確率で受け入れることにするのである。
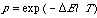
ここで、哿Eは微小変形によるエネルギーの増加量、T は温度に相当するパラメタである。これは Metropolis のモンテカルロ法で最初に使われた考え方で、熱平衡状態の分布関数を表しており、この条件の下に微小変形を繰り返すと系は熱平衡状態に達するのである。シミュレーテッドアニーリングでは、まず高温から始め、一定温度で Metropolis モンテカルロを十分に行って熱平衡に達したら温度を少し下げ、次の Metropolis モンテカルロを行うことを繰り返す。この手続きには数学的基礎があり、Metropolis モンテカルロを無限長の間行い、下げる温度の幅が無限小であれば、必ずグローバルミニマムに到達できるとされている。しかし現実にはどちらも有限でなければならないので、実用的なクーリングスケジュール(cooling schedule)を設定しなければならない。シミュレーテッドアニーリングは確率的な解法であるため長時間の計算を要するが、他の近似解法である程度のマルチプルアライメントを作り、それをさらに精密化する場合などには有効であろう。